Fork me on GitHub

(译)用 Isabelle/HOL 验证分布式系统

发表于 | 分类于 |
字数统计: 3.4k | 阅读时长 ≈ 12min
众所周知，分布式系统很难推理，正确性的正式证明对于分布式算法很有价值。

用 Isabelle/HOL 验证分布式系统

我们每天都以互联网服务的形式使用分布式系统。这些系统很有用，但实现起来也很有挑战性，因为网络是不可预料的。每当你发送一条网络消息的时候，它有可能很快到达，也有可能延迟很久，或者永远不会达到，又或者多次到达。

当你向另一个进程发送请求但没有收到响应时，你完全不知道发生了什么：是这个请求丢失了，还是另一个进程崩溃了，或者是响应丢失了？或者可能没有任何东西丢失，消息只是延迟了，还没有到达。没有办法知道发生了什么，因为进程通信的唯一方式是不可靠的消息传递。

分布式算法在这个不可靠的交流模型之上建立了一个更强大的保证。这种更强大的保证的例子包括数据库的事务和复制（在多台机器上维护一些数据的副本，以便当其中一个机器宕机时，数据不会丢失）。

不幸的是，众所周知，分布式系统很难推理。因为不论消息到达的顺序如何，他们都必须维护他们的保证，甚至是在一些消息丢失，或者一些进程奔溃的时候也如此。。许多算法非常微妙，非正式的推理不足以确保它们是正确的。此外，并发活动可能出现的排列和交织的数量，很快就变得太多，以至于模型检查器无法进行详尽的测试。出于这个原因，正确性的正式证明对于分布式算法很有价值。

在 Isabelle/HOL 中建模一个分布式系统

在这篇博文里，我们将会探索怎么样使用 Isabelle/HOL 辅助证明，去正式地验证一些分布式算法。Isabelle/HOL 没有对分布式计算有任何内置的支持，不过幸运的是，可以十分简单的使用 Isabelle/HOL 提供的结构：方法，列表和集合，去建模一个分布式系统。

首先，我们假设在系统里每一个进程（或节点）都有一个唯一的标识符，它可以简单的是一个整数或是一个字符串。根据算法，系统中一组进程 ID 可能是固定的和已知的，或者是未知的和不固定的（后者适用于进程们随时可以加入或离开的系统）。

然后算法的执行以离散的时间步长进行。在每个时间步长中，一个事件发生在其中一个进程上。这个事件可能是这三件事中的一个：接收一个其他进程发送过来的消息，接收用户的输入或者是超时。

1
2
3
4
datatype ('proc, 'msg, 'val) event
  = Receive (msg_sender: 'proc) (recv_msg: 'msg)
  | Request 'val
  | Timeout

被这些事件之一触发，进程会执行一个方法，可能会更新自己的状态并向其他进程发送信息。在一个时间步长发送的消息，可能会被在未来任何的时间步长接收到，或者可能完全不会被接收到。

每个进程都有一个不与任何其他进程共享的本地状态，这个状态在执行开始的时候是固定的初始值，并且只有当进程执行的时候更新。一个进程无法读取另一个进程的状态，但我们可以将整个系统的状态描述为所有进程的各个状态的集合：

图片

为什么线性的时间步长序列就足够了？

尽管真实的进程可能是并发运行的，我们不需要对并发进行建模，因为进程之间的交流只有发送和接收消息，并且我们可以假设一个进程在开始处理下一个事件之前完成了一个事件的处理。因此，每个并行执行都等价于一些线性的执行步骤序列。分布式系统的其他规范，例如 TLA+ 语言 ，也使用这种线性的步骤序列。

我们不对哪个时间步由哪个进程执行任何假设。进程可以公平地轮流运行，但同样有可能一个进程执行一百万次，而另一个进程什么也不做。通过避免对进程活动的假设，我们确保算法无论系统中的时间如何都能正常工作。例如，一个暂时与网络断开连接的进程仅由一个没有经历任何接收消息事件的进程建模，即使其他进程继续发送和接收消息也是如此。

在这个模型里面，一个进程的宕机只表示它在某个时间步长后不会再执行更多的步骤了；没有必要明确表示宕机。如果我们想让进程从宕机中恢复，我们可以添加第四种类型的事件来模拟崩溃后重新启动的进程。一个进程可以在崩溃后重新启动。当执行这样的崩溃恢复事件时，进程会删除其本地状态中存储在不稳定的内存中的任何部分，但保留其状态中稳定存储（在磁盘上）中的那些部分，在宕机中会幸存下来。

当推理算法安全属性时，最好不要假设哪个进程在哪个时间步执行，因为这样可以确保算法可以容忍任意消息延迟。如果我们想要推理存活（比如，算法最终终止），我们将不得不做出一些公平假设，比如说每一个未崩溃的进程最终会执行一个步骤。然而，在我们的证明里面，我们只聚焦在安全属性上。

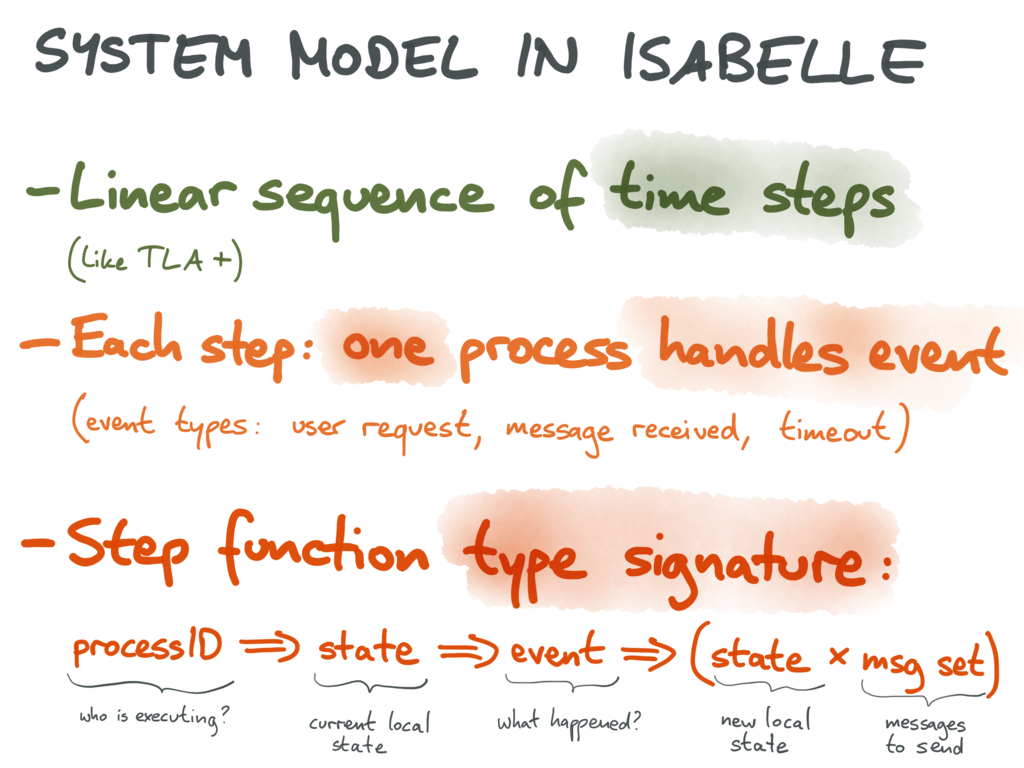
System model: linear sequence of time steps; at each step, one process handles an event

现在我们可以将一个分布式的算法表示为 step function ，它接受三个参数：执行当前时间步长的进程的 ID、该进程的当前本地状态和已发生的事件（消息接收、用户输入、超时，或崩溃恢复）。返回值包含该进程的新状态，以及一组要发送到其他进程的消息（每条消息都标记有接收进程的 ID ）。

1
2
3
type_synonym ('proc, 'state, 'msg, 'val) step_func =
  ‹'proc ⇒ 'state ⇒ ('proc, 'msg, 'val) event ⇒
  ('state × ('proc × 'msg) set)›

进程在一个时间步骤的当前状态等于它在前一步骤之后的新状态（或者如果没有前一步骤，则为初始状态）。进程在一个时间步的当前状态等于同一进程在前一步之后的新状态（就是初始的状态）。假设 step 函数是确定性的，我们现在可以把系统里任何一个执行编码为（进程 ID ，事件）键值对的集合，表示发生的一系列事件，以及它们发生在哪个进程。系统的最终状态是通过一次调用一个事件的阶跃函数来获得的。

去定义可能发生了什么

为了证明分布式算法的正确性，我们需要证明它在每次可能的执行中产生正确的结果，也就是说对于每一个可能的（进程ID，事件）键值对集合。但哪一种执行是可能的？只有一件事是我们可以安全地假设的：如果一个进程接收到一条消息，那么该消息一定已经发送到该进程。换句话来说，我们假设网络不会凭空捏造消息，并且一个进程不能模拟另一个进程。（在攻击者可以注入虚假数据包的公共网络中，我们必须对消息进行加密验证以确保此属性，但现在让我们将其排除在范围之外。）

因此，我们将做出的唯一假设是，如果在某个时间步长接收到消息，那么它一定是在前一个时间步长发送的。然而，我们会允许消息丢失、乱序或者是接收多次，让我们在 Isabelle/HOL 中编码这个假设。

首先，我们定义一个函数来告诉我们单个事件是否可能发生：如果事件 evt 被允许在系统中的进程 proc 中发生，(valid_event evt proc msgs) 会返回 true ，msgs 是迄今为止已发送的所有消息的集合。 msgs 是（发件人、收件人、消息）的三元组。在整个系统里。我们定义一个接受事件是允许出现的，如果接收的消息是在 msgs 和 Request 或者 Timeout 事件中，则允许事件发生，或者允许事件随时发生。

1
2
3
4
5
6
7
fun valid_event :: ‹('proc, 'msg, 'val) event ⇒ 'proc ⇒
                    ('proc × 'proc × 'msg) set ⇒ bool›
where
  ‹valid_event (Receive sender msg) recpt msgs =
    ((sender, recpt, msg) ∈ msgs)› |
  ‹valid_event (Request _) _ _ = True› |
  ‹valid_event Timeout _ _ = True›

接下来，我们定义所有可能的事件序列集合。为此，我们在 Isabelle 中使用了一个归纳断言：如果 events是算法执行中的有效事件集合，step是阶跃函数， init 是每个进程的初始状态，proc是系统中所有进程的集合（如果我们希望允许任意数量的进程，这可能是无限的），那么 (execute step init procs events msgs states) 返回 true 。最后两个参数跟踪执行状态：msgs 是迄今为止发送的所有消息的集合，states 是从进程 ID 到该进程状态的映射。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inductive execute ::
  ‹('proc, 'state, 'msg, 'val) step_func ⇒ ('proc ⇒ 'state) ⇒
   'proc set ⇒ ('proc × ('proc, 'msg, 'val) event) list ⇒
   ('proc × 'proc × 'msg) set ⇒ ('proc ⇒ 'state) ⇒ bool›
where
  ‹execute step init procs [] {} init› |
  ‹⟦execute step init procs events msgs states;
    proc ∈ procs;
    valid_event event proc msgs;
    step proc (states proc) event = (new_state, sent);
    events' = events @ [(proc, event)];
    msgs' = msgs ∪ {m. ∃(recpt, msg) ∈ sent.
                       m = (proc, recpt, msg)};
    states' = states (proc := new_state)
   ⟧ ⟹ execute step init procs events' msgs' states'›

该定义规定，当系统处于初始状态且未发送任何消息时，空事件列表有效。此外，如果 events 是迄今为止有效的事件序列，并且 event 在当前状态下是允许的，那么我们可以调用 step 函数，添加它发送到 msgs 的任何消息，更新相应进程的状态，其返回值是另一个有效的事件序列。

这就是我们建模一个分布式系统所需要的全部！

证明一个算法正确性

现在我们可以用一些算法（由它的阶跃函数和初始状态定义），并证明对于所有可能的事件列表，某些属性 P 成立。由于我们没有规定时间步长的最大值，因此可能的事件列表是无限的。但这不是问题，因为我们可以对列表使用归纳法来证明 P 。

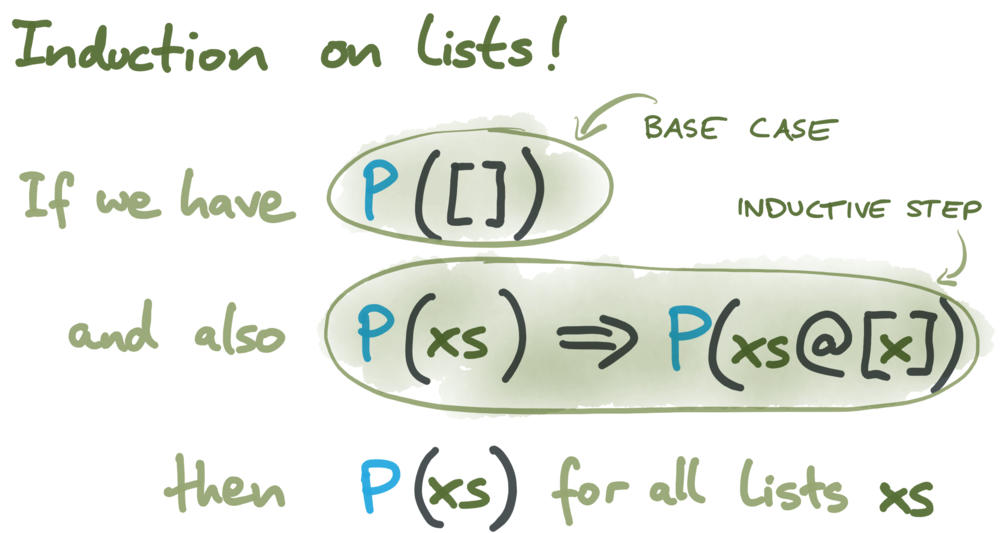
The Isabelle/HOL induction principle over lists

我们使用在 Isabelle/HOL 里 List.rev_induct 里的归纳规则。它要求证明：

  1. 对于空集合，属性 P 的值为真 (比如系统处于初始化状态，还没有执行任何节点);
  2. 如果属性 P 对于某些执行为真，我们在执行结束时再添加一个时间步长，那么 P 在该时间步长之后仍然成立。

换句话说，我们证明 P 在整个系统所有可能的状态中是一个不变量。在 Isabelle 里，这证明看起来是粗糙的像这个 ( step、 init、和 procs 被适当地定义过):

1
2
3
4
5
6
7
8
9
10
11
theorem prove_invariant:
  assumes ‹execute step init procs events msgs states›
  shows ‹some_invariant states›
using assms proof (induction events arbitrary: msgs states
                   rule: List.rev_induct)
  case Nil
  then show ‹some_invariant states› sorry
next
  case (snoc event events)
  then show ?case sorry
qed

验证分布式算法的真正挑战是提出正确的不变量，它既是值为真又暗示了你希望算法具有的属性。不幸的是，必须手动设计这个不变量。然而，一旦你有了一个不变量作为候选，Isabelle 对检查它是否正确，以及它是否强大到可以满足你的目标非常有帮助。

有关如何在此模型中证明简单共识算法的正确性的更多详细信息，我录制了一个2 小时的视频讲座 ，该讲座贯穿了第一原理的演示（无需之前有 Isabelle 的经验）。这个演示的 Isabelle 代码也是可用的。

如果发现译文存在错误或其他需要改进的地方，欢迎到 掘金翻译计划 对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

掘金翻译计划 是一个翻译优质互联网技术文章的社区，文章来源为 掘金 上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注 掘金翻译计划、官方微博、知乎专栏。